Mitä yhteistä on suomalaisella jalkapallolla ja Kiinan keisarin nenällä? Tarinan mukaan Kiinan keisarilla oli valtava nenä. Ongelma oli, että kukaan ei ollut koskaan nähnyt keisaria. Koska asiaan haluttiin kuitenkin ratkaisu, nenän pituutta kysyttiin miljoonalta kiinalaiselta. Vastauksista saatu keskiarvo oli Kiinan keisarin nenän pituus.

Saattaa kuulostaa hölmöläisten toimilta, mutta ei ole hirvittävän kaukana tavasta, jolla suomalaista jalkapalloa kehitetään. Meillä painottuu se, minkä kulloinkin ajatellaan olevan merkityksellistä: toistomäärät, pihapelit tai tasoryhmät. Yksi asia kuitenkin pysyy. Kenelläkään ei ole mitään hajua vastauksensa oikeellisuudesta, koska jalkapallosta puuttuu vaikuttavuusanalyysi.

Vaikuttavuusanalyysi tarkoittaa niiden toimenpiteiden kartoittamista, jotka tutkitusti vaikuttavat tehokkaimmin haluttuun asiaan. Esimerkiksi oppimisesta voidaan haluta tietää, vaikuttaako siihen tehokkaimmin luokan koko, tuntien pituus vai valittu opetusmetodi. Oppimisen tutkiminen on kuitenkin vaikeaa, sillä ensin tuloksista pitää poistaa normaali kasvun vaikutus. Luultavasti nimittäin kaikki oppilaat osaavat keväällä enemmän kuin edeltävänä syksynä lukuvuoden alkaessa. Se, että oppii, ei tarkoita että oppisi tehokkaasti. Oppimisen tutkiminen etenee hitaasti, koska siinä pitää muuttaa vain yhtä asiaa kerralla. Vasta kun tämä on tehty riittävän monta kertaa, voidaan sanoa, onko jokin tehokasta vai ei.

Suomalainen jalkapallo hakee menestystä nyt eikä aikaa vaikuttavuusanalyysiin tietenkään ole. Tuskin on haluakaan. Se tarkoittaisi käytännössä sen myöntämistä, että emme voi edes teoreettisesti menestyä nykyisellä sukupolvella, koska heidän avullaan tulisi ainostaan etsiä vaikuttavuudeltaan parhaita valmennusmetodeja. Jos mitään ei kyetä oppimaan jalkapallossa tehdyistä (hyvistä ja huonoista) toimenpiteistä, ehdotan että otetaan oppia koulumaailmassa tehdystä vaikuttavuusanalyysistä.

The Economist julkaisi artikkelin, jossa vertailtiin eri opetusmenetelmien vaikuttavuutta suhteessa niiden hintaan.¹ Kolme tehokkainta menetelmää olivat myös listan halvimpia. Oppilaan opettajalta saama palaute, oman osaamisen arviointi ja oppilaiden toisilleen antama vertaistuki vaikuttivat kaikkein eniten oppimistulokseen. Esimerkiksi opettajien suhteellisen määrän lisääminen pienentämällä luokkakokoja tai palkkaamalla tukiopettajia olivat kalliita, mutta vertailussa tehottomia menetelmiä. Kuriositeettina mainittakoon että tasoryhmiin jako (streaming by ability) vaikutti oppimiseen negatiivisesti.

The Economist nosti esille myös opettajien väärät kuvitelmat omista kyvyistään. Suurin osa opettajista nimittäin luuli, että opettaminen on taito, jonka kanssa synnytään, vaikka tutkimus osoittaa, että taito pääosin opitaan. Koska opettajat luulevat olevansa synnynnäisesti hyviä opettamaan (omat taidot pääosin yliarvoidaan), he käyttävät hyvin vähän aikaa itsensä kehittämiseen.

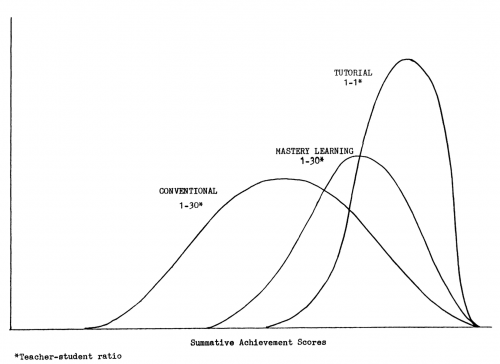
Benjamin Bloom ryhmineen vertasi perinteistä opetusmenetelmää (opettajan ja oppilaiden suhde 1:30) henkilökohtaiseen opettajaan (opettajan ja oppilaan suhde 1:1). Tulokset olivat hätkähdyttäviä [2]. Selvisi, että kun käytettiin henkilökohtaista opettajaa, 50 % oppilaista oppi saman, minkä perinteisessä opetuksessa oppi 2 % (Kuva 1). Toisin sanoin, tuhannesta oppilaasta 500:lla on potentiaalia oppia sama, minkä perinteisessä opetuksessa oppii vain 20 oppilasta. Vaikka henkilökohtaista opettajaa ei voidakaan käytännössä järjestää, Bloom osoitti kuinka suuri merkitys opetuksella on.

Mittaamiseen liittyy aina epävarmuus. Et voi esimerkiksi mitata omaa pituuttasi millimetriä tarkemmin, koska mittanauha ei sitä salli. Toisaalta et voi mitata pituuttasi edes senttimetrin tarkkuudella, koska olet aamulla pidempi kuin illalla (voit todeta asian mittaamalla pituutesi makuulla ja seisaalla). Mittaamiseen liittyvän epävarmuuden suuruudesta saadaan kuva toistamalla mittaus useita kertoja. Tai, koska saman asian oppimista voi mitata vain kerran, toistamalla mittaus useammalla oppilaalla.

Kun toistomittauksia on tehty riittävästä, ja jokainen tulos sijoitettu x-akselille ja sen esiintymistiheys y-akselilla, saadaan kellon muotoinen käyrä (Kuva 1). Käyrän laki on mittauksen keskiarvo ja samalla sen todennäköisin tulos. Käyrän leveys kuvaa mittauksen epävarmuutta ja sen nimi on keskihajonta. Karkeasti voidaan sanoa, että mitä vähemmän käyrien pinta-alat ovat päällekkäin, sitä todennäköisempää on, että mittausten keskiarvot eroavat toisistaan.

Jos kyse on erittäin tärkeästä asiasta, tutkijat asettavat hyvin tiukat rajat tulosten luotettavuudelle. Esimerkiksi Higgsin bosonin (fysiikan alkeishiukkanen) löytäneet tukijat toistivat mittauksen kunnes oli olemassa yksi mahdollisuus 3,5 miljoonasta, että havainto on vain sattuma. Todennäköisyydeltä vastaava tapahtuma sattuisi kerran maanviljelyn keksimisen jälkeisessä historiassa (8 500 vuotta).

Kuva 1. Oppimistulosten jakautuminen perinteisessä (conventional) ja henkilökohtaisessa (tutorial) opetuksessa. Keskiarvojen erotus on kaksi keskihajontaa [2].

Bloomin ryhmän tekemien havaintojen mukaan perinteisen opetuksen ja henkilökohtaisen opettajan ero oppimistuloksessa oli keskimäärin kaksi keskihajontaa. Koska keskihajontaa merkitään symbolilla sigma, Bloom kutsui sen opetusmenetelmän etsintää, joka pääsee perinteisen opetuksen resursseilla lähimmäksi henkilökohtaista ohjaajaa, nimellä “the two sigma problem”. Toistaiseksi yksikään menetelmä ei ole osoittautunut yhtä tehokkaaksi kuin henkilökohtainen opettaja.

Yksi Bloomin tunnistama menetelmä, joka vastaa edellä esitettyyn kysymykseen on mastery learning (Kuva 1). Koska en ole perehtynyt Bloomin ratkaisun yksityiskohtiin, kuvaan sen sijaan suomalaisen Pekka Peuran yksilöllisen oppimisen menetelmää [3], jota hän käyttää matematiikan opetuksessa Martinlaakson lukiossa, ja joka perustuu Bloomin ajatuksiin. Pekan lähtökohta on, että perinteinen opetus, jossa kaikille opetetaan sama, on hyvin epätasa-arvoista. Menetelmä, jossa opettaja valitsee missä, miten ja koska oppilas oppii, sopii vain hyvin pienelle osalle oppilasta. Suurin osa ei joko ehdi oppia tai oppisi paljon nopeammin omia aikojaan. Lopputuloksena on vain turhautuneita oppilaita.

Yksilöllisen oppimisen menetelmässä oppilailla on mahdollisuuksia vaikuttaa siihen, miten ja missä he oppivat. Koska nopeimmin oppivat saavat edetä omaa vauhtiaan, heille jää myös aikaa syventää omaa osaamistaan opettamalla hitaammin oppivia. Yksilöllisen oppimisen menetelmässä arvioinnin tarkoitus ei ole pistää oppilaita järjestykseen, vaan tunnistaa oppilaan osaaminen. Tämä tarkoittaa sitä, että oppilas ja opettaja arvioivat jatkuvasti oppilaan osaamista, ja eteenpäin siirrytään vasta, kun yksi opeteltava aihe on riittävän hyvin hallussa.

Perinteisessä arvioinnissa oppilas tekee kokeen jakson lopussa, eikä kokeen lopputulos millään tavalla vaikuta siihen, mitä seuraavaksi tapahtuu. Ajatelkaapa jos vastaavaa menetelmää sovellettaisiin talonrakennukseen. Urakoitsija saisi kaksi viikkoa aikaa tehdä perustukset, jonka jälkeen rakennusmestari arvioisi ne. Arvosana voisi olla vaikka seiska, koska betoni ei ehtinyt kuivua ja osa rakennustarvikkeista jäi saapumatta. Arvosanalla ei kuitenkaan olisi mitään merkitystä, vaan rakentamista jatkettaisiin suunnitelman mukaan seinien pystyttämisellä.

Video 1. Pekka Peura selittää yksilöllisen oppimisen mallia.

John Hattie on australialainen tutkija, joka on kollegoineen käynyt läpi 250 miljoonaa kouluikäistä lasta vastatakseen kysymykseen mikä toimii ja mikä ei toimi opetuksessa. Hattien listan tärkein luku on 0,4. Hattie nimittäin havaitsi, että kaikkien opetusmenetelmien keskimääräinen vaikutus on sen suuruinen. Niinpä hän päätti valita sen vertailuluvukseen. Jos opetusmenetelmän vaikutus on pienempi kuin 0,4, sitä ei kannata käyttää, koska se on keskimääräistä heikompi. Jos taas vaikutus on suurempi kuin 0,4, menetelmä on keskimääräistä parempi.

Hattien lista kertoo, että ryhmän tai tilan järjestämisellä, oppilaiden ominaisuuksilla tai teknologian käyttämisellä ei ole vaikutusta oppimiseen. Hattien listan ykkösenä on self-reported grades. Tässäkin kohtaa oma ymmärrykseni loppuu ja nojaan nyt puolestani Matti Räsäsen tulkintaan [4]: “Hattie tarkoittaa tällä sitä, että kun oppilaat tietävät mihin arvosanaan he tähtäävät, he motivoituvat tämän tavoitetason ylittymisestä. Opettajan tehtävä on selvittää mitkä ovat oppilaan tavoitteet ja auttaa häntä ylittämään ne. Opettajan tulee siis löytää oppilaan lähikehityksen vyöhykkeen rajat ja auttaa häntä ylittämään ne. Oppilaiden motivaatiota lisää, jos he tietävät pystyvänsä saavuttamaan asettamansa tavoitteet. Opettajan tehtävä on mahdollistaa tämä.”

Oman sisäisen motivaation löytyminen on luultavasti äärimmäisen tärkeää niille, jotka pääsevät huipulle koska ovat jaksaneet harjoitella tavoitteellisesti [5].

Video 2. John Hattie Norrköpingissä kertomassa mikä toimii ja mikä ei toimi opetuksessa.

Alle on listattu kysymystä, joihin suomalaisen valmennuksen pitäisi nykytietämyksen mukaan pystyä vastaamaan, jos haluamme jatkossa kehittää parempia pelaajia.

1. Miten saamme valmentajat pysymään lajin parissa pidempään, jotta heillä on riittäväsi aikaa kehittyä hyviksi valmentajiksi?
2. Minkä asetamme valmentajien motivaation lähteeksi? Jos valmentajat motivoituvat vääristä asioista kuten voittamisesta, he valitsevat helposti metodeja (mm. pelaajien rekrytointi), jotka johtavat haluttuun tavoitteeseen, mutta eivät kehitä pelaajia.
3. Minkä asetamme pelaajien arvioinnin tavoitteeksi: Laittaa pelaajat paremmuusjärjestykseen vai auttaa pelaajia tunnistamaan oma lähikehityksen vyöhykkeensä ja motivoitua oppimaan?
4. Kuinka osoitamme pelaajille ymmärrettävästi oppimisen tavoitteen?
5. Kuinka tuemme valmentajia antamaan parempaa palautetta tavoitteeseen etenemisestä?

Lähteet

1. The Economist, Education reform: Teaching the teachers. Luettu 27.7.2016. Saatavilla osoitteessa: http://www.economist.com/news/briefing/21700385-great-teaching-has-long-been-seen-innate-skill-reformers-are-showing-best
2. Benjamin Bloom, 1984, The 2 Sigma Problem: The Search for Methods of Group Instruction as Effective as One-to-One Tutoring, Educational researcher, 13(6), s. 4–16. Luettu 28.7.2016, saatavilla osoitteessa: http://web.mit.edu/5.95/readings/bloom-two-sigma.pdf
3. Pekka Peuran blogi. Luettu: 27.7.2016. Saatavilla osoitteessa: http://www.maot.fi
4. Matti Räsäsen blogi. Luettu 5.8.206. Saatavilla osoitteessa: http://hiyhtk.wordpress.com
5. Tim Rees ym., 2016, The Great British Medalists Project: A Review of Current Knowledge on the Development of the World’s Best Sporting Talent. Sports Medicine, 46(8), 1041-1058. [Linkki]